Eli Broemer
/E·Lye Bray·mer/
Abstract
Full PDFOptimizing Non-Linear Mechanical Behavior of Soft Tissues in Finite Element Model of Human Thigh
Eli Broemer (1), Sheng Chen (1), Justin Scott (1), Tamara R Bush (1), Sara Roccabianca (1)
(1) Mechanical Engineering
Michigan State University
East Lansing, MI, USA
INTRODUCTION
Pressure ulcers (PUs) are a soft tissue injury caused by sustained pressure and/or shear near a bony prominence, more commonly in the thigh and buttocks area [1]. The injury most commonly develops in those with reduced mobility such as hospitalized patients and wheelchair users. Formation of PUs can lead to pain, infection, and even death. A recent 10-year study found that PUs are prevalent in 9% to 13% of patients in health care facilities in the United States [2].
The clinical setting is also lacking effective prediction methods for PUs [1]. Specifically, an interpretive scoring evaluation is the widely recommended tool for assessing PU risk. And there is not strong evidence showing that scoring tools are more effective at reducing the risk of PUs when compared to a medical practitioner’s judgement alone.
Finite element methods estimating pressure distributions in soft tissues surrounding bony prominences may be used as a novel PU prevention tool for patients in the future. Such models have been previously developed in literature ranging from 2D linear models with 34 nodes [3] to detailed 3D non-linear models with over 250,000 nodes [4]. These commonly focus on the thigh and buttock region, so that the material properties of the bulk soft tissue in the area may be estimated.
A significant limitation to most of these thigh-buttock studies is lack of validation and error estimation, or the use of only two data points to validate highly non-linear material models (i.e. an unloaded and a body weight-bearing configuration) [4, 5].
This preliminary study aims to find the best fitting material parameters using a finite element model of a thigh whose geometry is generated from subject-specific MRI scans. The innovation is that the material parameters are estimated by comparing the model prediction with in vivo indentation tests at multiple load configurations. The goal of the model is to study the material behavior of soft tissues in seated individuals. Further research may investigate the material behavior as it relates to the prevention of PUs in wheelchair users.
METHODS
Experimental Setup. A single subject (Male, 185 lbs., 73 in.) participated for the purposes of this pilot study.
Force-deflection measurements were collected by indentation tests performed on the subject’s thigh. Since it is difficult to collect indentation data from the posterior thigh of a seated individual, a quadruped posture was adopted for this procedure. The quadruped position has the same hip and knee flexion as the sitting position with the advantage of access to the thigh for indentation tests.
To setup the quadruped posture, the subject kneeled on both legs behind a small panel placed to constrain the forward movement of the thigh. The panel height was short of the subject’s anterior superior iliac spine allowing them to lean forward, and a table in front of the panel supported their chest and head. The table was adjusted such that the subject’s knee and hip angles were ~ 90° to mimic the seated position.
Indentation tests gave force-deflection measurements of the thigh via a six-axis load cell and a linear potentiometer respectively. The deformation was applied manually at a constant rate, and the system was calibrated to have zero force and deflection when the indenter was flush with the undeformed thigh [6]. Three locations on the posterior thigh were tested (i.e., proximal, middle, and distal), and between 60 N and 100 N of force was applied before the indenter was removed.
Geometry Generation. MRI scans of the subject in a supine position provided cross-sectional data for the thigh geometry. The images were segmented with Photoshop CS6 (Adobe – 2012) in order to obtain cross-sections of the bone, muscle, and fat. Figure 1 shows 3D geometry for the three tissues, which was generated by interpolating the cross-sections in NX 12.0 (Siemens – 2017).
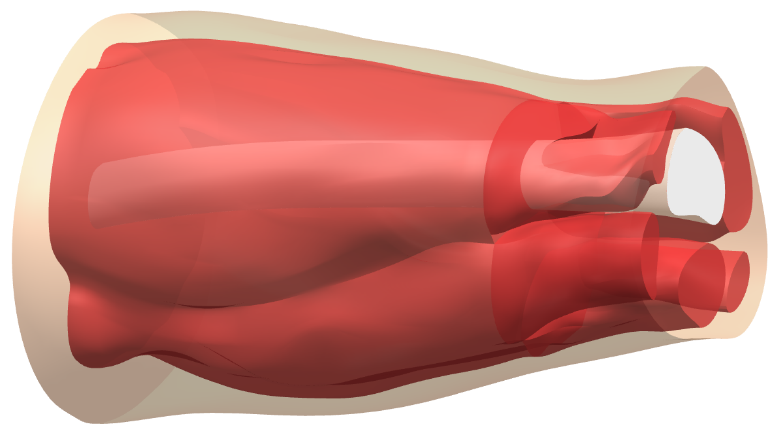
Figure 1: Geometry of subject’s left thigh. Leftmost plane is just after buttocks and rightmost plane is just before the kneecap.
Finite Element Model. The model was meshed in HyperMesh (Altair – 2017) with second order tetrahedral elements. The mesh had 58,848 elements and 85,272 nodes. The model was setup and solved with the FEBio suite [7].
A previous study by our research group showed that the first order Ogden material model can accurately represent the non-linear mechanical behavior of these soft tissues in vivo. Equation 1 shows the first order strain energy function for an Ogden material, where λi are the principle stretches, μ is a parameter with units of Pascals, and α is a unit-less parameter. Initial material parameters for the muscle and fat were taken from literature [4]. Soft tissues were assumed nearly incompressible (i.e., ν = 0.485) [5]. The femur was assumed to be a rigid body.
Four boundary conditions constrained the model solution: 1) the femur was fixed in all directions and rotations; 2) a no-slip constraint on all material contact surfaces; 3) the left and right planes in Figure 1 were fixed in their normal axis; 4) nodes with forces applied, at the three testing locations, had their movement constrained to the anterior - posterior axis (i.e. the direction of the force). Three load conditions were applied to model the mechanical test performed in vivo.
Optimization. The goal of the optimization protocol was to minimize the difference between the model force-deflection curves and the experimental data for each of the three test locations. A simplex search function (i.e., fminsearch) in MATLAB (MathWorks – 2018) minimized the objective function by adjusting material parameters μ and α and then re-solving the model in FEBio at each iteration.
Equation 2 shows the objective function where NRMSDprx, NRMSDmid, and NRMSDdis are the normalized root mean square deviations estimated for each of the three test locations.
RESULTS
Optimized material parameters were estimated by fitting the model to the in vivo experimental data (Table 1). The values of the material parameters are in reasonable agreement with recent studies investigating the same tissue behavior [4]. The first order Ogden model fit the experimental data well. Error, measured as the normalized root mean square deviations between the model and in vivo data, was 5.47%, 1.48%, and 9.96% for proximal, middle, and distal locations respectively (Figure 2).
DISCUSSION
This pilot study investigates the mechanical properties of fat and muscle tissues in the human thigh. An anatomically detailed FE model was used to determine optimized material parameters. This model represents the first attempt to inform a finite element thigh model by precise tissue geometry and non-linear in vivo experimental data.
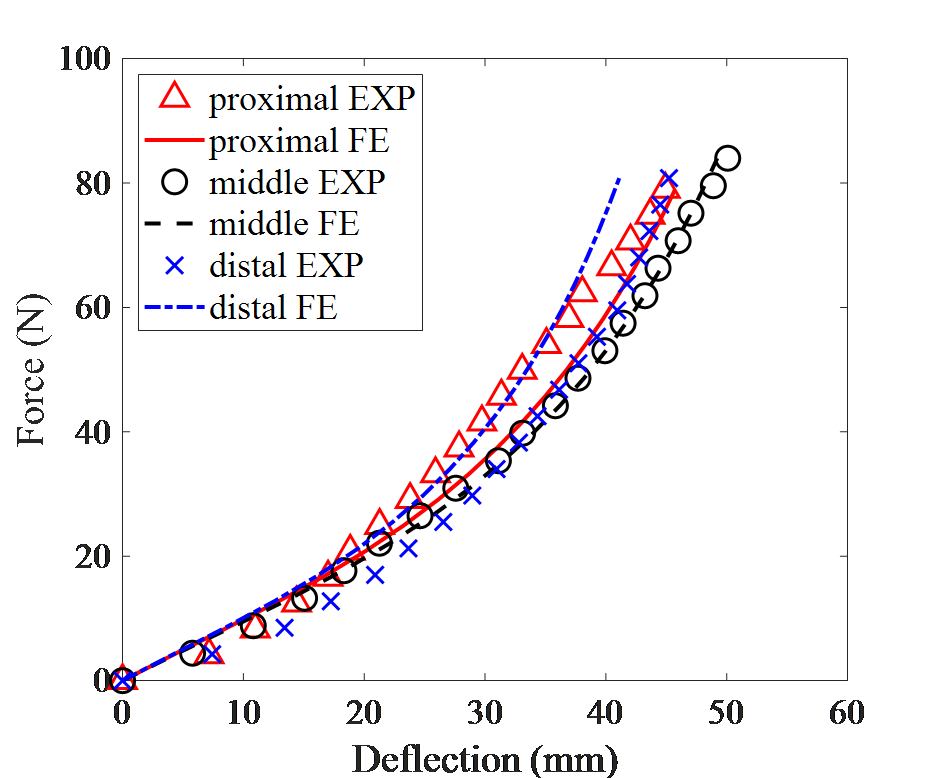
Figure 2: Simulated material behavior (continuous lines) fitted to non-linear in vivo indenter data (markers) for proximal, middle, and distal locations on the thigh.
Bulk material properties found in this study are limited to the thigh in a quadruped position. Model error was smallest in the middle thigh. Larger error at proximal and distal thigh locations may be due to the close proximity to fixed boundaries. Material contact surfaces assumed to have no slip could also affect the accuracy of this model, however there is sparse literature on this material interaction.
The optimization and model approach in this pilot study is useful to others interested in non-linear soft tissue mechanical behavior modeling.
Table 1: Initial and optimized materials parameters for this model
| Material Parameter | μ (kPa) | α | |
| Muscle | Initial | 1.91 | 4.6 |
| Optimized | 1.43 | 6.16 | |
| Fat | Initial | 1.17 | 16.2 |
| Optimized | 1.01 | 14.54 | |
ACKNOWLEDGEMENTS
NSF CBET 1603646
REFERENCES
[1] Qaseem, A et al., Ann Intern Med, 162(5):359-69, 2015. [2] VanGilder, C et al., J Wound Ostonomy Continence Nurs, 44(1):20-28, 2017. [3] Chow, WW et al., J Biomech Eng, 100(2):79-87, 1978. [4] Al-Dirini, RM et al., Ann Biomed Eng, 44(9):2805-16, 2016. [5] Makhsous, M et al., IEEE Trans Neural Syst Rehabil Eng, 15(4):517-25, 2007. [6] Sadler, Z et al., Int J Non-Linear Mech, 107:77-85. [7] Maas, SA et al., J of Biomech Eng, 134(1):011005, 2012.
SB3C2019
Summer Biomechanics, Bioengineering, and Biotransport Conference
June 25-28, Seven Springs, PA, USA
 Home
Home